Matematikoje terminai „skaitmuo” ir „skaičius” dažnai vartojami kasdienėje kalboje, tačiau šie terminai turi skirtingas prasmes. Supratimas apie jų skirtumus yra svarbus ne tik matematikos moksluose, bet ir kasdieniniame gyvenime, ypač susiduriant su skaičių įvedimu, skaitymu ir interpretavimu. Šiame straipsnyje išnagrinėsime, kas yra skaitmuo, kas yra skaičius ir kaip jie skiriasi vienas nuo kito.
Kas yra skaitmuo?
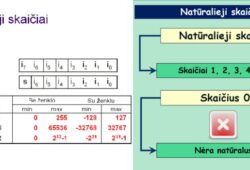
Skaitmuo yra simbolis arba ženklas, naudojamas skaičių reiškimui. Matematikoje paprastai naudojama dešimtainė skaitmenų sistema, kuri apima skaitmenis nuo 0 iki 9. Kiekvienas iš šių skaitmenų gali būti naudojamas atskirai kaip skaitmuo arba kartu su kitais skaitmenimis, kad būtų sudarytas skaičius. Pavyzdžiui, skaitmuo „3“ yra vienas iš dešimties pagrindinių skaitmenų, kuriuos naudojame norėdami sudaryti skaičius.
Kas yra skaičius?
Skaičius yra matematinė koncepcija, naudojama objektų kiekiui nustatyti, palyginti arba eilės tvarkai išdėstyti. Skaičiai sudaromi iš skaitmenų (arba skaitmenų), ir kiekvienas skaičius atspindi tam tikrą reikšmę. Skaičiai gali būti paprasti, pavyzdžiui, 2, 45, 678, arba sudėtingesni, pavyzdžiui, -23, 4.56, 3/4. Tai reiškia, kad skaičiai gali būti teigiami, neigiami, sveikieji, trupmeniniai, racionalieji ar netgi iracionalieji.
Apibendrinant
Pagrindinis skirtumas tarp skaitmens ir skaičiaus yra tas, kad skaitmuo yra vienas simbolis iš riboto skaitmenų rinkinio (pvz., 0–9 dešimtainėje sistemoje), naudojamas norint sudaryti skaičius, o skaičius yra visa reikšmė, galinti būti sudaryta iš vieno ar daugiau skaitmenų. Skaičiuotuvai naudoja skaitmenis skaičiams sudaryti ir atlikti įvairius matematinius skaičiavimus. Kai naudojate skaičiuotuvą, jame įvedate skaitmenis, kurie sudaro skaičius, pavyzdžiui, 123. Čia 1, 2 ir 3 yra skaitmenys, o jų derinys – skaičius 123. Skaitmuo yra skaičiaus statybinis blokas, o skaičius yra pilna matematinė koncepcija, kurią naudojame kasdieniame gyvenime ir matematikoje, siekdami nusakyti kiekybinius santykius ir atlikti skaičiavimus. Supratimas apie šių dviejų sąvokų skirtumus padeda aiškiau suvokti skaičių struktūrą ir jų naudojimą.
Šaltiniai: